The Logic Page Solving Quick Logic Puzzles Humans characteristically like to be challenged in physical or intellectual ways. These challenges do not need to be competitive, although that is very common. Challenges can also be private and personal. The individual accepts the challenge and then grows as a result of the encounter with something that isor wasdifficult. In a very basic way, Quick Logic Puzzles are no different from other intellectually stimulating games. Q.L.Puzzles are distinctive, however, because they are designed to maximize the mentally stimulating effect while minimizing the time it takes to achieve positive benefits. Q.L.Puzzles present us with a set of guesses and clues based on those guesses. Our goal is to solve a puzzle by using the guesses and clues in ways that allow us to determine the patterns that could be in the secret code. Our solution strategy should proceed in a systematic mannernot only to solve the puzzle but also to train the mind. This is part of the logic of the puzzles as well as of puzzle solving. Certain general questions will guide our reasoning: * Can we determine if the code contains specific elements and not others (referring here to specific numbers, but in some puzzle types, letters)? * How many of any particular element is present in the code? * In which order are the elements in their respective quantities? Answering these questions will require us to logically exclude some code elements from the range of possibilities, while also including others. On this Logic Page you will find one way to deduce the secret code or codes. Examples will be discussed systematically. Some terms should be defined first. * An element refers to a character (numeral or letter) in the code and the guess. There can be code elements and guess elements. * Position within a guess or the code will be conveyed via "p.1" for Position 1, etc., counting left to right. * Hits specify the number of correct elements in their correct spot in the code; hits will be designated as "H". Misplaced refers to the number of correct elements which are not in their correct place. (H:1, M:2 thereby identifies one hit and two misplaced elements). The total number of hits and misplaced, of course, sum to 4 in a Q.L.Puzzle with four elements. * If an element in the hidden code could match more than one of the same element in the guess, then the priority goes to that guess element which is a hit. (For example: comparing the guess 5-1-2-2 with the code 5-5-3-4 will yield H: 1, M:0, because the first 5 in the guess is correctly placed as the first element in the secret code; there are no misplaced guess elements relative to the code).
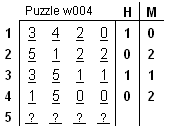
(Q. L. Puzzle w004 is repeated from above)	An Example of "Puzzling Logic" I have set down several steps through which we can deduce the codeor the range of plausible guesses about the codefor Q.L.Puzzle w004 (to the left and repeated below). What follows is more a way to "read" a puzzle than a sure-fire procedure for solving all such puzzles. Yet understanding my logic will hopefully provide some guidance in the decoding process. Initially, I determine the "Givens": what the clues say about the guess in relation to other guesses/clues. Then, I reason about what the givens tell me about which elements are where in the code in what quantities (the "Thuses"). * Initial Conditions: The Puzzle Itself. Q.L. Puzzle w004 is what I call a "4R6 puzzle". There are 4 elements in the code/guess which are drawn from a range of 6 elements (0, 1, 2, 3, 4, 5). Repeated elements are possible in the code (hence, 5-5-5-5, 1-2-3-4, and 5-2-2-4 could all be the secret code). Before any guess is made, there are 1296 combinations, any of which could be the code (1296 = 6 elements x 6 x 6 x 6). Each clue of Hits and Misplaced narrows the number of potential combinations of code elements. The key to deducing the code is to use all clues in light of all guesses, and thereby figure out which combination of elements are included and which are excluded. * Reasoning Step A. Given: Guess[2] of Puzzle w004 (5-1-2-2) indicates that there are two misplaced elements and that the element 2 in Position.3 (p.3) of Guess[2] does not corroborate the 2 in p.3 of Guess[1] (3-4-2-0). (Had there been a 2 in the code, then Guess[2] would have exhibited at least one hit.) Thus: There cannot be a 2 in the code, as indicated by Guess[2]. Thus, by implication: The elements 5 and 1 are in the hidden code, but not in their correct spots. * Reasoning Step B. Given: The clues, H:1 and M:1, of Guess[3] (3-5-1-1) refer only to one 5 and one 1 (see Reasoning Step A). Thus: Guess[3] indicates that there is only one 1 in the code. Thus: There is no 3 in the code. * Reasoning Step C. Given: The clues for Guess[4] (1-5-0-0), which are H:0; M:2, indicate that only two elements of the actual code were in the guess. Given: Elements 5 and 1 are somewhere in the code (see Reasoning Step A). Thus: We deduce that there is no 0 in the code. Thus: The element 5 in p.2 and the element 1 in p.1 are in the wrong positions. Thus: We are confronted with a question. In our reasoning, which element do we hold constant in its position? The 5 in p.2? Or a 1 in either p.3. or p.4? * Reasoning Step D. Given: There is no 3 (see Reasoning Step B), no 2 (reasoning step A), and no 0 (see reasoning step C). Thus: The 4 from Guess[1] is the last possible element of the hidden code; it is definitively situated in p.2. * Reasoning Step E. Given: After 4 guesses we are certain that the elements 1, 5, 4 are in the code. As regards the quantity of each distinctive element: Given: There is only one 1 (as implied by Guess[3]). Given: The 5 cannot be situated in p.1 or p.2 (as implied by Guess[2] and Guess[4], respectively). Given: The 1 cannot be situated in p.1 or p.2 (as implied by Guess[4] and Guess[2], respectively). Thus: There must be two 4s: one in p.2 (as indicated in Guess[1]), and one in p.1 (as deduced via implication, because both p.3 and p.4 will be occupied by either element 5 or element 1). * Reasoning Step F. Given: From the four sets of clues (for Guesses[1-4]) we cannot determine conclusively whether element 1 is situated in p.3 or p.4. Given: Likewise, from the four sets of clues we cannot logically exclude element 5 from being placed in either p.3 or p.4. THUS: For Quick Logic Puzzle w004, there exist two possible solutions at Guess[5]: the hidden code is either 4-4-5-1 or 4-4-1-5. Of course, it is quite possible to solve puzzlesand have fun, toowithout following such a process.
	© 2004 R. W. Williams